1. Interaction effects in the zoo of topological state of matter
We make use of large-scale quantum Monte Carlo simulations and field theoretical analysis to study interacting fermion systems and pursue the understanding of interaction effects on topological state of matter, such as the validity of topological index in the interaction-driven topological phase transitions (Phys. Rev. B 93, 195163 (2016), Phys. Rev. B 93, 195164 (2016)), the emergent bosonic symmetry protected topological phase in an interacting fermion model (Phys. Rev. B 94, 165121 (2016), see the left figure), and the novel bulk phase transition associated with topological term in the quantum field theory description (Phys. Rev. B 93, 115150 (2016)).
Moreover, the duality relation between the interaction-driven topological phase transition and the
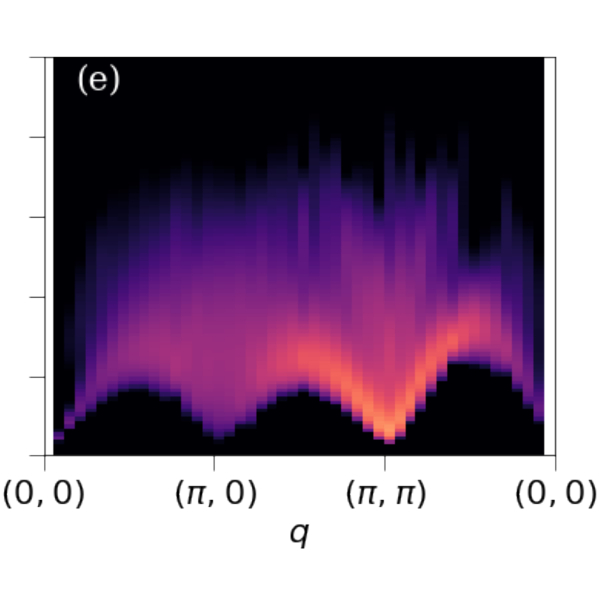
deconfined quantum critical point has been revealed recently by us via our numerical investigations (Phys. Rev. X 7, 031052 (2017), see the middle figure).Quantum spin liquids, as representatives of topological ordered states, have also been discovered by our large-scale quantum Monte Carlo simulations on frustrated spin systems (arXiv:1711.03679, see the right figure), and the manifestation of the symmetry fractionalization in these symmetry enriched topological phases (arXiv:1701.01552).
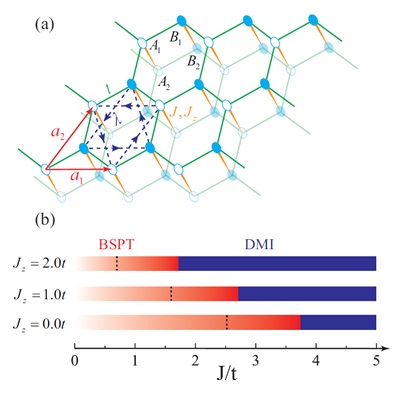
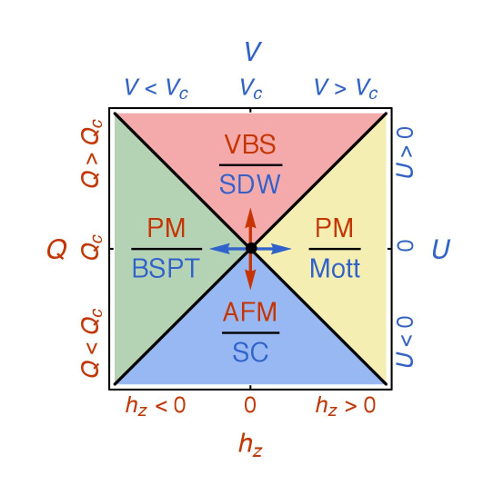
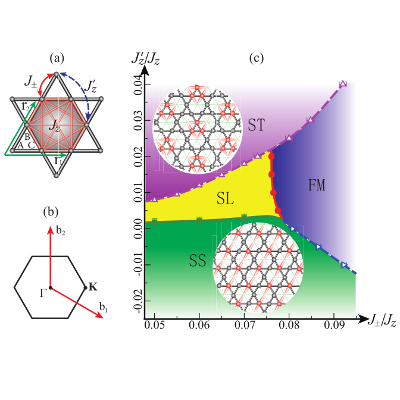
2. Quantum phase transitions in new paradigm
We employ large-scale quantum Monte Carlo simulations, i.e., stochastic series expansion and worm-algorithm in the path-integral framework, to pursue the understanding of quantum phase transition and novel quantum phases in the (frustrated) quantum magnetic systems, within and more importantly beyond the Landau-Ginzburg-Wilson paradigm. Examples encompass the logarithmic corrections and amplitude (Higgs) mode in the (3+1) D O(3) antiferromagnet to dimer-singlet quantum phase transition (Phys. Rev. B 92, 214401 (2015), Phys. Rev. Lett. 118. 147207 (2017), see the left figure),
the Coulomb U(1) quantum spin liquid phase in the frustrated XXZ model on the pyrochlore lattice (Phys. Rev. Lett. 115, 037202 (2015), arXiv:1707.00099 (PRL accepted), see the middle figure), the Z2 quantmum spin liquid phase in the frustrated XXZ model on the kagome lattice and the symmetry fractionalization therein (arXiv:1701.01552, arXiv:1711.03679).
Moreover, by means of quantum Monte Carlo simulation plus stochastic analytic continuations, we are able to reveal the dynamic signature of fractionalization of spinons and emergent gauge fields at the deconfined quantum critical points (arXiv:1803.01180, see the right figure).
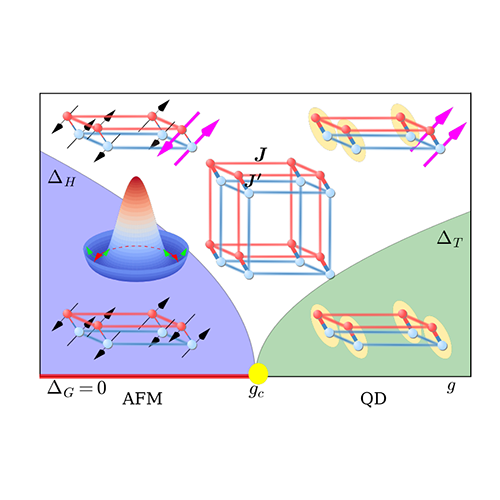
3. Fundamental properties of metallic quantum critical point
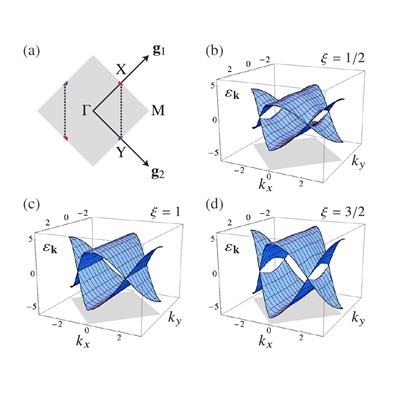
We are developing new quantum Monte Carlo scheme, that incorporate the critical bosonic fluctuations to Fermi surface or Fermi point in an unbiased manner, such that the long-standing problem of the metallic quantum critical point can be addressed without approximation. Our attempt in anisotropic velocity fluctuations of Dirac fermions (arXiv:1602.07150, and see the left figure) has revealed rich phase diagram that contains topological phase transition and enhanced SO(4) fermion bilinear fluctuations in the dynamically degenerated nodal lines. Investigations of bosonic flucutations on a full Fermi surface are on-going.
